++ 50 ++ lim x tends to 0 log(1 x)/3^x-1 300704-Lim x tends to 0 log(1+x)/3^x-1

View Full Answer log3 to the base e2 ;KCET 13 displaystyle limx → 0 ( loge(1x)/3x1) = (A) log e3 (B) 0 log 3e (D) 1 Check Answer and Solution for above question from Mathemat$$\lim_{x \to 0}x^x =1$$ Hence $$\log \mathrm L=\lim_{x \to 0}x^x \log x=\lim_{x \to 0}1 \cdot \log x=\infty$$ $$\implies \mathrm L=0$$ If you want to know why is $\displaystyle\lim_{x \to 0}x^x =1$, rewrite it as $\displaystyle\lim_{x \to 0}{e^{x \ln x}}$ and for that limit, See this

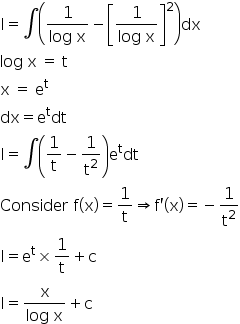
Integration 1 Log X 1 Log X 2 Dx Explain In Great Detail And Give Full Solution Mathematics Topperlearning Com D8cj2ett

Lim x tends to 0 log(1+x)/3^x-1

Lim x tends to 0 log(1+x)/3^x-1-What is limit x tends to 0 log(1x)/x to the base a?2/5 lim_{x to 0}(log(5x)log(5x))/x qquad = lim_{x to 0}(log(5x)log 5 log 5 log(5x))/x qquad = lim_{x to 0}(log(5x)log 5)/x (log(5(x))log 5)/(x

Limit Of 1 2x 1 X As X Goes To 0 L Hospital S Rule Youtube

N=1 are also points on the graph of the function f(x) = 1/x for x > 0 As x gets larger, f(x) gets closer and closer to zero In fact, f(x) will get closer to zero than any distance we choose, and will stay closer We say that f(x) has limit zero as x tends to infinity, and we write f(x) → 0 as x → ∞, or lim x→∞ f(x) = 0 5 10 x 0Ans is 07 ;Learn how to evaluate the limit of 1sinx whole power of quotient of 1 by x as x approaches zero in fundamental and advanced methods in calculus

We have limit ( logx/x) as x approaches to infinity Now putting the value of x=infinity ,then logx=log infinity=infinity So limit (logx/x) as x tends to infinity, is in infinity/infinity form According to Lhospital's rule,limit( 1/x) as x tends to infinity is 1/x=1/infinity ie equal to zeroLim x> 0 (cotx 1/xCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history

Lim x0 {log(1x^3) * x^3} / (sinx)^3 * x^3 lim x0 log(1 x^3) / x^3 * lim xo x^3 / (sinx)^3 1 * 1 = 1 I'm sure that would help you!!Click here👆to get an answer to your question ️ If log 03(x 1)X Well begun is half done You have joined No matter what your level You can score higher Check your inbox for more details {{navliveTestEngineeringCount}} Students Enrolled {{navliveTestMedicalCount}} Students Enrolled Start Practicing

Step By Step Math Wolfram Alpha Blog

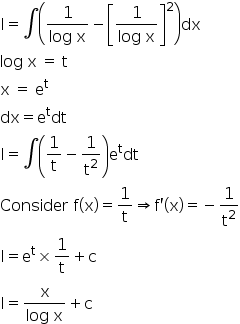
Integration 1 Log X 1 Log X 2 Dx Explain In Great Detail And Give Full Solution Mathematics Topperlearning Com D8cj2ett

Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions toSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreOn substituting we get form, so solve it using L'spital rule Apply derivative to numerator and denominator and then apply limit The solution of

Step By Step Math Wolfram Alpha Blog

Limits

 · x^(1/x) I was wondering whether there was an easier way to prove that this tends to 1 as x tends to infinity Can we not just focus on this part first 1/x We can definitely show that this tends to 0 as x tends to infinity and so due to this no matter what x^(1/x) Will tend to 1 as its power tends to 0Dear Aditya, The value tends to 1 Cracking IIT just got more exciting,It s not just all about getting ass · All the conditions for using l'Hopital's rul for this "0/0" case are met So lim x>0 ln(1x) / x = lim x> (1/(1x)) / 1 = 1 Alternatively, for small x ln(1x) ≈ x x^2 / 2 x^3/3 So the fraction is 1 x/2 x^2/3 , which clearly goes to 1 for x to zero

Control System Mcq Multiple Choice Questions Javatpoint

Step By Step Math Wolfram Alpha Blog

Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queries Students (upto class 102) preparing for All Government Exams, CBSE Board Exam, ICSE Board Exam, State Board Exam, JEE (MainsAdvance) and NEET can ask questions from any subject and get quick answers byCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyExcept that 0instead of the indeterminate 0form 0 we instead have ∞ As before, we use the exponential and natural log functions to rephrase the problem 1/x ln x 1 /x ln x x = e = e x Thus, lim x 1/x ln= lim e x x Since the function et is continuous, x→∞ x→∞ ln x ln x lim e x = e lim x→∞ x x→∞ ln x

Limit Of Sin X X As X Approaches 0 Video Khan Academy

Evaluate The Following Limit Lim X 0 Log 1 X 3 X 1

Free limit calculator solve limits stepbystep This website uses cookies to ensure you get the best experience(log(x) 1)/(xe) =log (x/e)/e((x/e)1)now using lim (x>0)log(x1)/x =1as x/e >1 and x/e 1 >0we get 1/eIf lim(x→0) (1 x log(1 b^2))^1/x = 2b tan^2θ, b > 0 and θ ∈ (–π, π), then the value of θ is asked Nov 15, 19 in Limit, continuity and differentiability by Raghab (504k points) limits;

Integrate Log 1 X 1 X2 Dx Upper Limit 1 Lower Limit 0 Maths Integrals Meritnation Com

If L Lim X 0 Asinx Bx Cx 2 X 3 2x 2log 1 X 2x 3 X 4 Exis

 · Find an answer to your question lim x tends to 0 (1x)^1/x e / x is equal toI'm going to hazard a guess that what was meant was $\log x \log(x1)$ One can write $\log x \log(x1) = \log \dfrac x {x1}$ and then \begin{align} \lim_{x\to · Get an answer for 'lim x> 0 (cotx 1/x ) Find the limit using L'Hospital's Rule where appropriate If L'Hospital's Rule does not apply, explain why ?

Evaluate The Following Lim X Tends To 2 1 X 2 2 2x 3 X3 3x2 2x Maths Limits And Derivatives Meritnation Com

F X 2x 2 16 4x 16 If X 2 At X 2 K If X 2 Studyrankersonline

Lim X → 0 Log ( 1 X ) 3 X − 1 Department of PreUniversity Education, Karnataka PUC Karnataka Science Class 11 Textbook Solutions 71 Important Solutions 3 Question Bank Solutions 5819 Concept Notes & Videos 515 Syllabus Advertisement Remove all ads Lim XEvaluate limit as x approaches 0 of ( natural log of 12x)/x Evaluate the limit of the numerator and the limit of the denominator Tap for more steps Take the limit of the numerator and the limit of the denominator Evaluate the limit of the numerator Tap for more steps Take the limit ofIn this tutorial we shall discuss another very important formula of limits, \\mathop {\lim }\limits_{x \to 0} \frac{{{a^x} 1}}{x} = \ln a\ Let us consider the

Lim X Tends To 0 Loge 1 5x X Brainly In

The Value Of Lim X Rightarrow 0 Frac Log Left 1

Log base 3 e6 Limx0 log(13x)/3^x1 Limx0 log(13x)/3x ÷ (3^x1)/x×3 3 ÷log3Lim x>0 log(1x)/3 x1 Share with your friends Share 0 0 is the answer8 ;We know that But i Similarly ii Adding i and ii which means that the value of x lies in the interval 0,2 But there's a problem, when sine is 0 cosine is 1, they might even be 0 and 1 at particular points (not in this case, since they are even powers), so the minimum we would get should be more than 0

Evaluate Limit X Tends To 1 E X 1 Root Over 1 Cosx Brainly In

Algebra Of Limits Study Material For Iit Jee Askiitians

Show transcribed image text EXERCISES 21 Exer 110 Find the limit 1 lim x tends to 2 (3x1) 3 lim x tends to 4 x 5 lim x tends 100 7 7 lim x tends to 1 Pi 9 lim x tends to 1 x4/2x1 · Alternatively, x may approach p from above (right) or below (left), in which case the limits may be written as → = or → = respectively If these limits exist at p and are equal there, then this can be referred to as the limit of f(x) at p If the onesided limits exist at p, but are unequal, then there is no limit at p (ie, the limit at p does not exist)Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more

Gamma Beta Functions 1

What Is The Limit As X Approaches 0 From The Right Hand Side Of Ln X Socratic

1109 · lim e^(ln(x^x)) x > 0 Use the log property to move the x outside of the log lim e^x ln(x) x > 0 Move the limit inside of the exponent e^ lim (x ln(x)) x > 0 Now the limit is of the form 0*infinity, which is indeterminate Let's move x to the denominator as (1/x) e^ lim ( ln(x)/(1/x) ) x > 0 How the form is infinity · lim x>0 log(3x) log(3x) /x applying De l ' Hospital's Rule ilm x>0 f(x)/g(x) = lim x>0 { f'(x)/ g('x) } so= lim x>0 1/3x *(1) 1/3x *1/1 · Ex 131, 6 Evaluate the Given limit lim┬(x→0) ((x 1)5 −1)/x lim┬(x→0) ((x 1)5 − 1)/x = ((0 1)5 −1)/0 = (15 − 1)/0 = (1 − 1)/0 = 0/0 Since it

Ex 13 1 9 Evaluate Lim X 0 Ax B Cx 1 Chapter 13 Class 11

Lim X Tends To 0 1 X 1 X E X Is Equal To Brainly In

Lim x → a (axxa/xxaa)=1 , then (A) a=1 (B) a=0 a=e (D) none of these Check Answer and Solution for above Mathematics question Tardigrade · When a linear asymptote is not parallel to the x or yaxis, it is called an oblique asymptote or slant asymptoteA function f(x) is asymptotic to the straight line y = mx n (m ≠ 0) if → () () = → () () = In the first case the line y = mx n is an oblique asymptote of ƒ(x) when x tends to ∞, and in the second case the line y = mx n is an oblique asymptote of ƒ(x) when xClick here👆to get an answer to your question ️ x→0 (cosecx)^1/logx is equal to

The Value Of Lim X Gt0 Sinx 1 X 1 X Sinx Youtube

Find The Limit As X Goes To 1 Of 1 Log X 1 X 1 Stumbling Robot

 · tex\lim_{x\to 0} \int_0^1 \frac{dt}{1 xt}= \int_0^1 \lim_{x\to 0}\frac{dt}{1 xt}/tex which, while true, probably requires deeper math than uman, who has not yet dealt with L'Hopital's rule or power series, has availableWe will use the limit #lim_{k\to 0} \frac{\ln(1k)}{k} = 1# I didn't use #x# on purpose, since I want to emphasize the idea behind this exercise is is important that you have the same quantity inside the logarithm (after the "one plus") and at the denominator, no matter what that expression is, as long as it tends to zero Some may even prefer writingSOLUTION 1 = = 0 (The numerator is always 100 and the denominator approaches as x approaches , so that the resulting fraction approaches 0) Click HERE to return to the list of problems SOLUTION 2 = = 0 (The numerator is always 7 and the denominator approaches as x approaches , so that the resulting fraction approaches 0) Click HERE to return to the list of

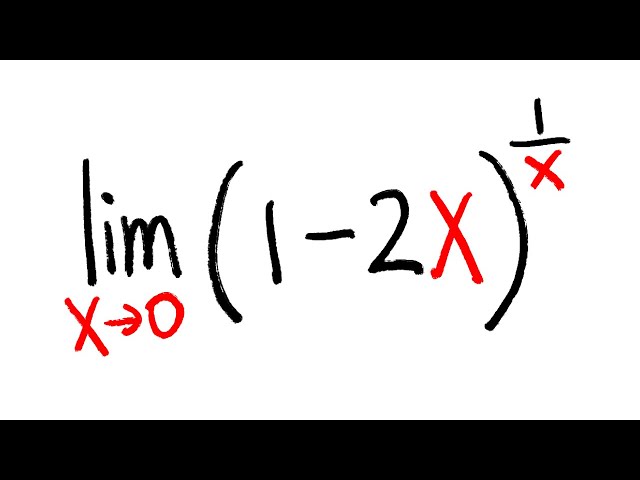
Limit Of 1 2x 1 X As X Goes To 0 L Hospital S Rule Youtube

How Can We Find Out The Limit X Tends To Infinity Log X X Quora

Answer to Evaluate the limit as x approaches infinity of x^(1/x) By signing up, you'll get thousands of stepbystep solutions to your homeworkIn These sums put yhe value of x like in first question tanx/x when x tens 0 is 1 and i/x2 becomes infinity ie it is of the form 1 raised to the infinity a simple formula is Lt x tends 0 f(x)^g(x) where it is of the form 1^inf is equal to e^Lt x tends 0 ((f(x) 1)/G(x)) for first it becomes e^ ( lt x tends 0 tanx x/x$\displaystyle \large \lim_{x \,\to\, 0}{\normalsize \dfrac{\ln{(1x)}}{x}}$ Actually, the limit of this type of rational function is equal to one as the input of the function tends to zero This standard result is used as a formula while dealing the logarithmic functions in limits

Epsilon Delta Definition Of A Limit Brilliant Math Science Wiki

Calculus I Limits At Infinity Part Ii

A question from limitsIf we directly evaluate the limit \lim_{x\to 3}\left(\frac{62x}{x^23x}\right) as x tends to 3, we can see that it gives us an indeterminate form We can solve this limit by applying L'Hôpital's rule, which consists of calculating the derivative of both the numerator and the denominator separatelyEvaluate limit as x approaches 0 of (3^x1)/x Take the limit of each term Tap for more steps Apply L'Hospital's rule Tap for more steps Evaluate the limit of the numerator and the limit of the denominator Tap for more steps Take the limit of the numerator and the limit of the denominator

A Lim X 0 1 Cos2x E X 2 E X X Equals Sarthaks Econnect Largest Online Education Community

Ex 13 1 6 Evaluate Lim X 0 X 1 5 1 X Class 11

Calc final in 2 hours, it's cram time ( Thanks so much for the help! · What is the limit as x approaches 0 for the equation e^2x / x Can you also show steps, if possible?`lim_(x > 0)(2^x 1)^3/((3^x 1)*sinx*log(1 x))` = `lim_(x > 0)((2^x 1)^3/x^3)/(((3^x 1)*sinx*log(1 x))/x^3) ("Divide numerator and"),("denominator by

Example 3 Evaluate I Lim X 1 X15 1 X10 1 Chapter 13

Evaluate The Limit Limx 0 Log 1 X 3 X 1 Sarthaks Econnect Largest Online Education Community

Limits At Infinity Infinite Limits And Asymptotes

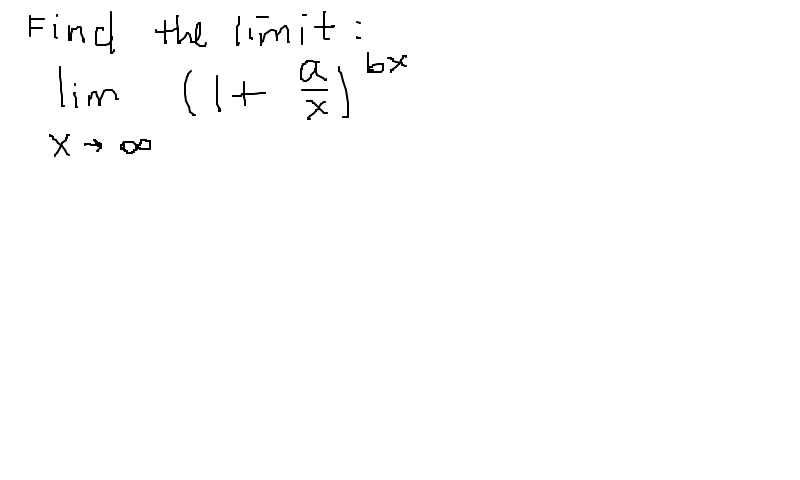
What Is The Limit As X Approaches Infinity Of 1 A X Bx Socratic

Evaluating Lim Limits X To 0 1 X 1 X Mathematics Stack Exchange

Evaluate The Following Limits If Exist Lim X 0 Log 1 X 3 Sin 3x Sarthaks Econnect Largest Online Education Community

Use Of Infinitesimals

How To Solve Lim X 0 1 X 1 X 2 E 1 X Quora

Limits At Infinity Infinite Limits And Asymptotes

What Is The Value Of Sin X Log 1 X X 2 Limit X Tending To 0 Quora

Limits

Limit As X Approaches Infinity For Log Of Greatest Integer Over X Youtube

Lim X Tends To 0 Log 6 X Log 6 X X Log 6 X A Log 6 X 80 Lim 1 2 Solution We Have Maths Limits And Derivatives Meritnation Com

The Value Of Lim X Rightarrow 0 Frac Log Left 1 A X B X 2 C X 3

Limits

Lim X Gt 0 Log 3 X Log 3 X X K Then The Value Of K Is Brainly In

F X Sin A 1 X Sinx X X Lt 0 C X 0 Root Of X Bx 2 Root Of X Bx 3 2 X Gt 0 Mathematics Topperlearning Com 5gbkb9bb

Lim X 0 E X 1 X Formula

What Is The Answer To Math Lim X To 0 Bigl Frac Tan X X Bigr 1 X 2 Math Quora

Evaluate Lim X Tends To 1 Log 1 X 2 Cotpx Brainly In

If Lim X 0 Log 3 X Log 3 X X K The Value Of K Is Sarthaks Econnect Largest Online Education Community

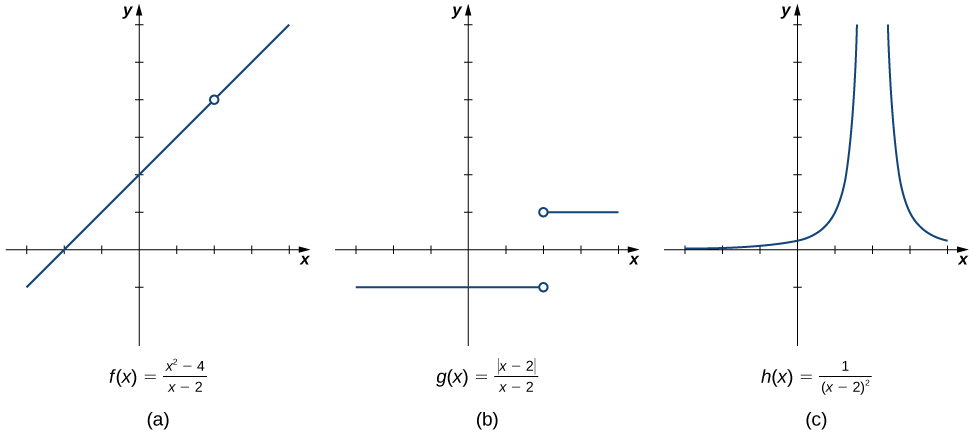
2 2 The Limit Of A Function Calculus Volume 1

Solved I Need Help With These 3 7 And 13 Only Step By Chegg Com

Limit Of Sin X Cos 1 X As X To 0 Mathematics Stack Exchange

Prove That Lim X To 0 Sqrt 1 X 1 Log 1 X 1 2

Algebra Of Limits Study Material For Iit Jee Askiitians

In Two Different Ways Prove The Limit As X Tends To 0 Of Log 1 X X Is 1 Stumbling Robot

Lim X 0 2 7 X 9 X 3 X 1 Sqrt 2 Sqrt 1 Cosx

Evaluate Limit X Tends To 0 1 X 6 1 1 X 5 1 Maths Limits And Derivatives Meritnation Com

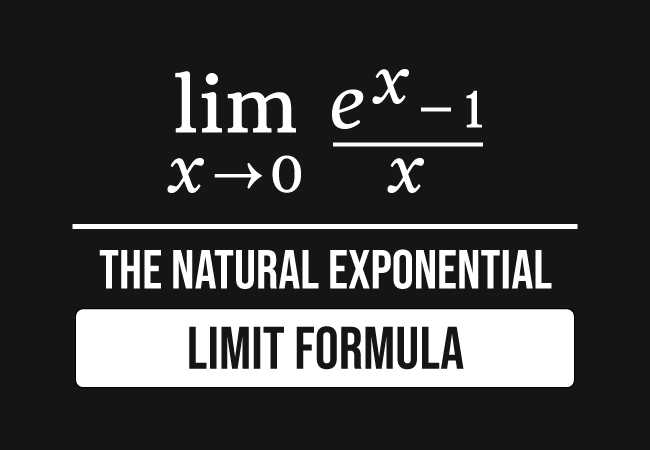
Lim X 0 E X 1 X Formula

Evaluate Lim X 0 Log 1 3x Log 1 2x Sarthaks Econnect Largest Online Education Community

Divergence Of The Sum Of The Reciprocals Of The Primes Wikipedia

Example 2 Find Limits I Lim X 1 X 2 1 X 100 Teachoo

Proof The Derivative Of Ln X Is 1 X Video Khan Academy

Evaluate X 1x 7 2x 5 1 X 3 3x 2 2

Sin 1 X And X Sin 1 X Limit Examples

L Hopital S Rule Wikipedia

Solved Or Every Ned 4 4 5 Evaluate The Following Limits Chegg Com

Evaluate Lim X 0 Xe X Log 1 X X 2 Sarthaks Econnect Largest Online Education Community

Ex 13 1 23 Find Lim X 0 And Lim X 1 Where F X 2x 3 3 X 1

X 1 1 X 1 31 X 2 3 Maths Questions

Rd Sharma Solutions For Class 11 Chapter 29 Limits Download Free Pdf Available

How To Evaluate Math Lim X To Infty X 1 X Math Quora

Prove That Lim Tend To 0 Log 1 X 3 Sin 3x 1plz Answer Brainly In

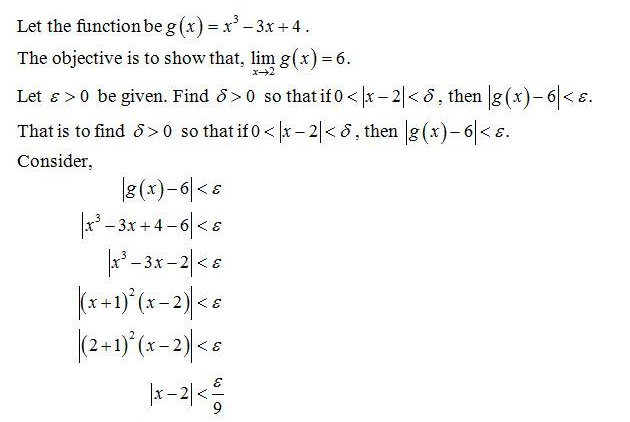
Solved Could Anyone Draw The Graph For This Soultion Chegg Com

Limit Of 1 X 1 X As X Approaches 0 Youtube

Lim X Gt0 E X 1 Log 1 X Sinx

14 2 Limits And Continuity

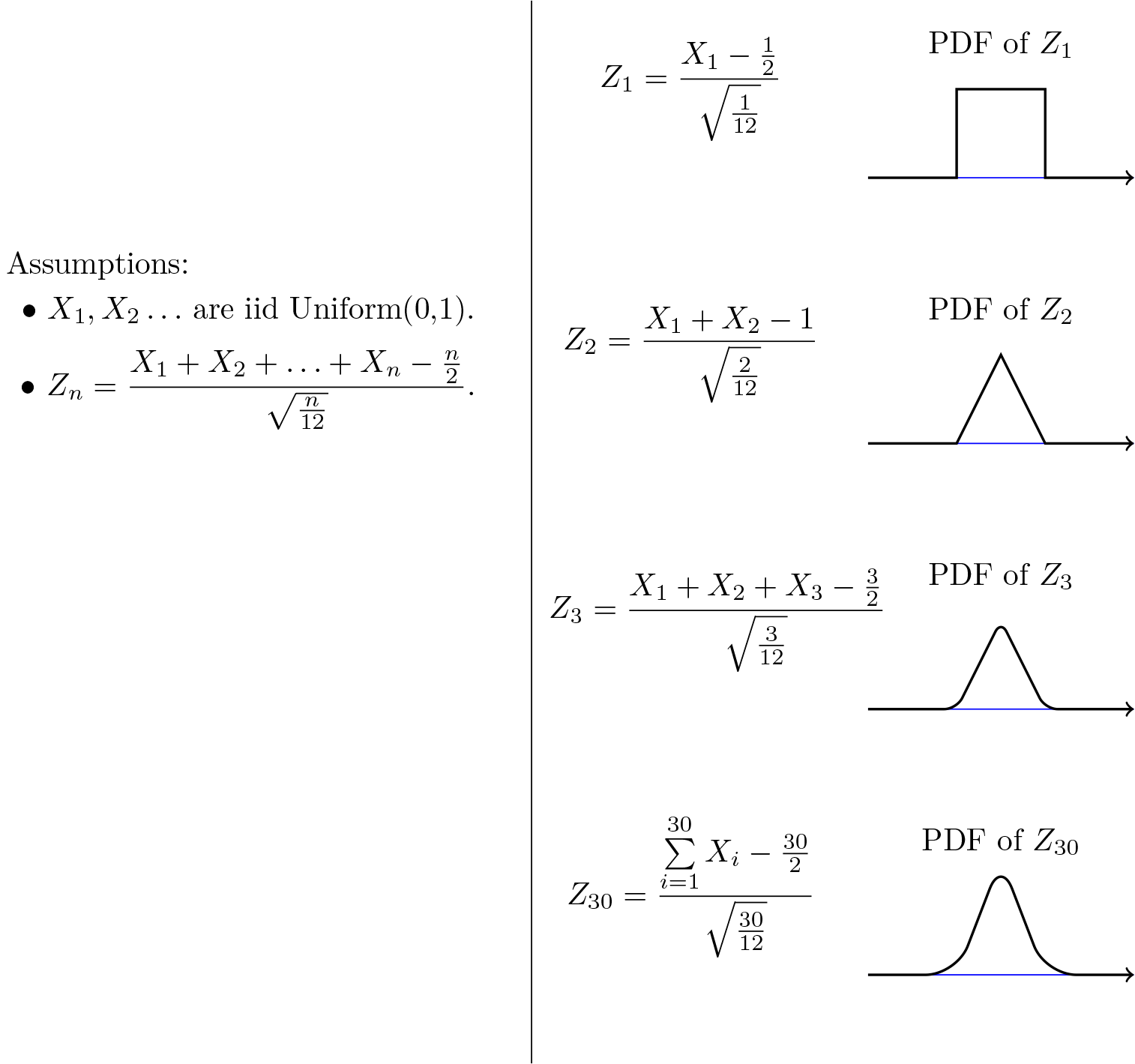
Central Limit Theorem

Integrate Sin 1x 1 X2 3 2 Dx Studyrankersonline

Find Lim Tends To 0 Log 1 X 3 Sin 3x Brainly In

Lesson 18 Indeterminate Forms And L Hopital S Rule

Limit Of 1 Cos X X As X Approaches 0 Video Khan Academy

How To Prove That Lim Limits X To0 Frac Sin X X 1 Mathematics Stack Exchange

Example 3 Evaluate I Lim X 1 X15 1 X10 1 Chapter 13

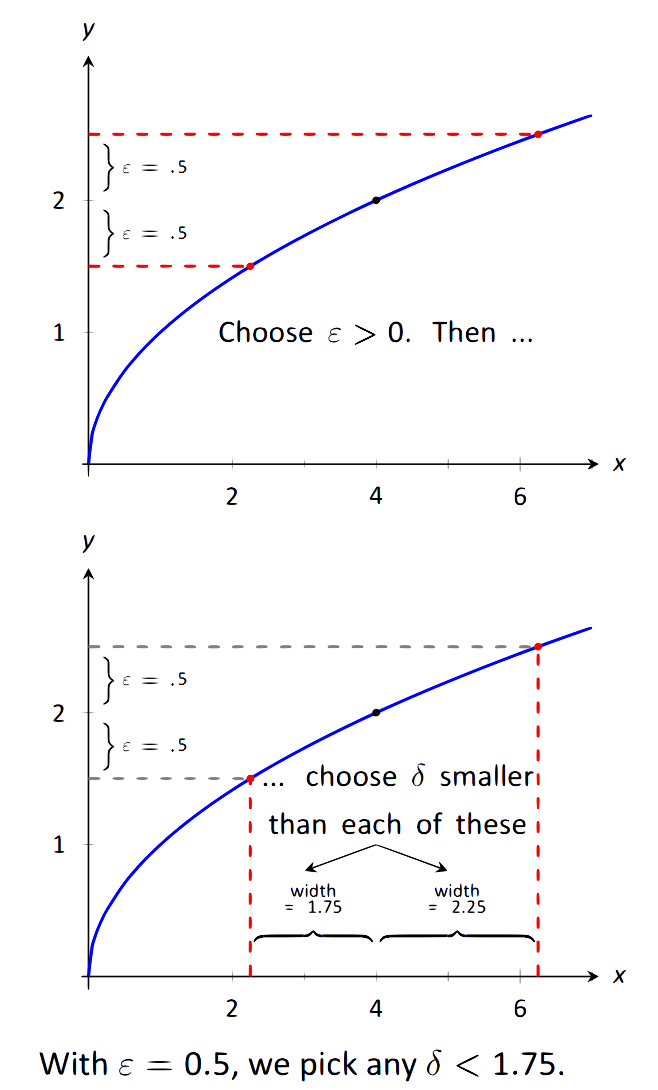
1 2 Epsilon Delta Definition Of A Limit Mathematics Libretexts

What Is Solution Of This Question Lim X Tending To 0 Log 1 3x 2 X E 5x 1 Quora

L Hopital S Rule Limit At 0 Example Video Khan Academy

Indeterminate Form Wikipedia

Lim X 0 Sin 3 Sqrtx Log 1 3x Tan 1 Sqrtx 2 E 5sqrtx 1

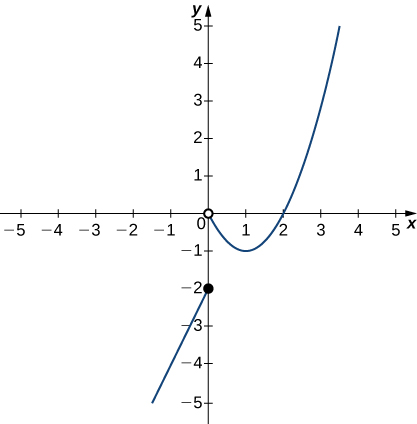
2 2 The Limit Of A Function Calculus Volume 1

Definition Of Derivatives To Prove Limit Ln 1 X X 1 Youtube

Lesson 18 Indeterminate Forms And L Hopital S Rule

Incoming Term: lim x tends to 0 log(1+x)/3^x-1,